DDX7 - Franco Caspe

DDX7: Differentiable FM Synthesis of Musical Instrument Sounds
Franco Caspe - Andrew McPherson - Mark Sandler
Queen Mary University of London - Centre for Digital Music
Paper - Code - Presentation Video

Abstract

FM Synthesis is a well-known algorithm used to generate complex timbre from a compact set of design primitives. Typically featuring a MIDI interface, it is usually impractical to control it from an audio source. On the other hand, Differentiable Digital Signal Processing (DDSP) has enabled nuanced audio rendering by Deep Neural Networks (DNNs) that learn to control differentiable synthesis layers from arbitrary sound inputs. The training process involves a corpus of audio for supervision, and spectral reconstruction loss functions. Such functions, while being great to match spectral amplitudes, present a lack of pitch direction which can hinder the joint optimization of the parameters of FM synthesizers. In this paper, we take steps towards enabling continuous control of a well-established FM synthesis architecture from an audio input. Firstly, we discuss a set of design constraints that ease spectral optimization of a differentiable FM synthesizer via a standard reconstruction loss. Next, we present Differentiable DX7 (DDX7), a lightweight architecture for neural FM resynthesis of musical instrument sounds in terms of a compact set of parameters. We train the model on instrument samples extracted from the URMP dataset, and quantitatively demonstrate its comparable audio quality against selected benchmarks.

Architecture

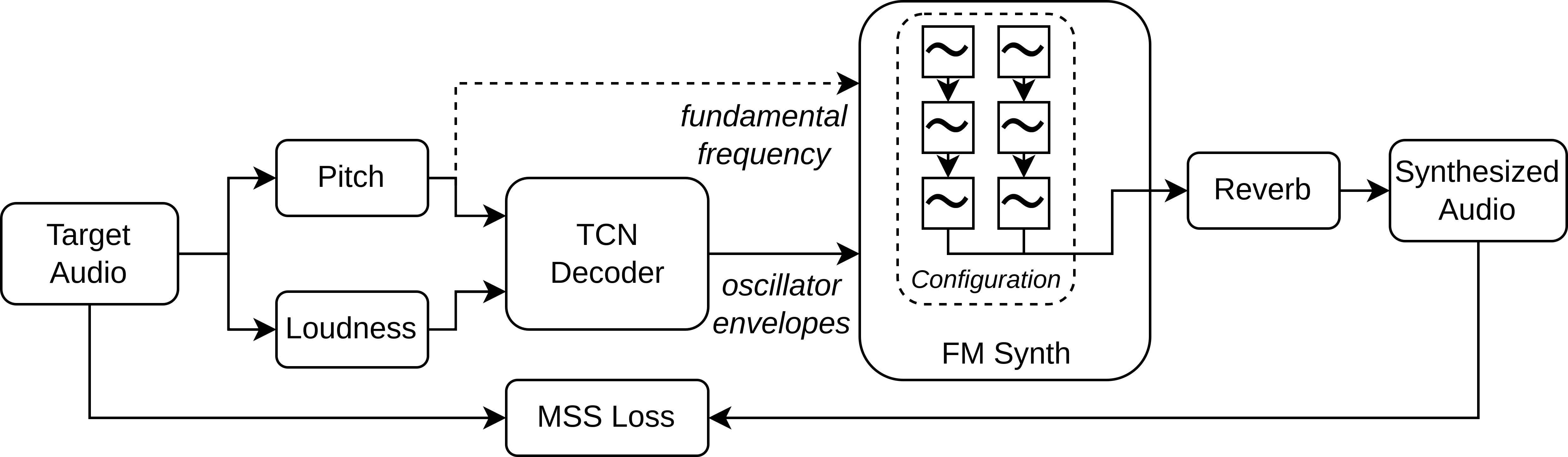
Figure 1: The DDX7 architecture employs a TCN decoder conditioned on a sequence of pitch and loudness frames to drive the envelopes of a few-oscillator differentiable FM synthesizer that features a fixed FM configuration with fixed frequency ratios, effectively mapping continuous controls of pitched musical instruments to a well-known synthesis architecture.

Continuous Control of an FM Synthesizer

We show resynthesis results on unseen data for the best scored DDX7 models according to the Frechet Audio Distance[1]. We compare the results with the Harmonic plus Noise (HpN) baseline model (a Pytorch implementation of the DDSP Decoder[2]), and the original recordings extracted from the URMP[3] dataset.

Instrument	Original	HpN Baseline	DDX7
Violin			6 Oscillators. I_max = 2
Flute			6 Oscillators. I_max = 2
Trumpet			2 Oscillators. I_max = 2π

Table 1: We show that for our resynthesis tasks, even with few oscillators, Differentiable FM can achieve a performance comparable to a more complex spectral modeling synthesis architecture.

Intervenable Synthesis Process

FM is a well-known synthesis architecture that features a compact set of sound design parameters. Once DDX7 is trained, such parameters can be modified on-the-fly to alter the model’s output. Here we present a set of simple and temporally static transformations as a proof of concept. We leave for future work a thorough exploration of these affordances.

Model	Intervention	DDX7 Resynthesis	Intervened Result
Violin 6 oscillators. I_max = 2	Tripled all modulator ratios of value 1.
Flute 6 oscillators. I_max = 2	Doubled modulators' envelope amplitudes.
Trumpet 2 oscillators. I_max = 2π	Modulator ratio changed to √2.

Table 2: By performing simple FM transformations, users can generate new timbre without re-training the model.

Hyperparameters

In DDX7, the maximum modulation index that the oscillators can take (I_max), and the FM configuration that is selected in the differentiable synthesizer, are important hyperparameters that have an impact on the convergence of the model. We present resynthesis audio excerpts generated during the two evaluations we conducted to assess their agency on the final results.

6-oscillator configurations

Ablated configurations

Figure 2: FM configurations evaluated for the different instruments tested.

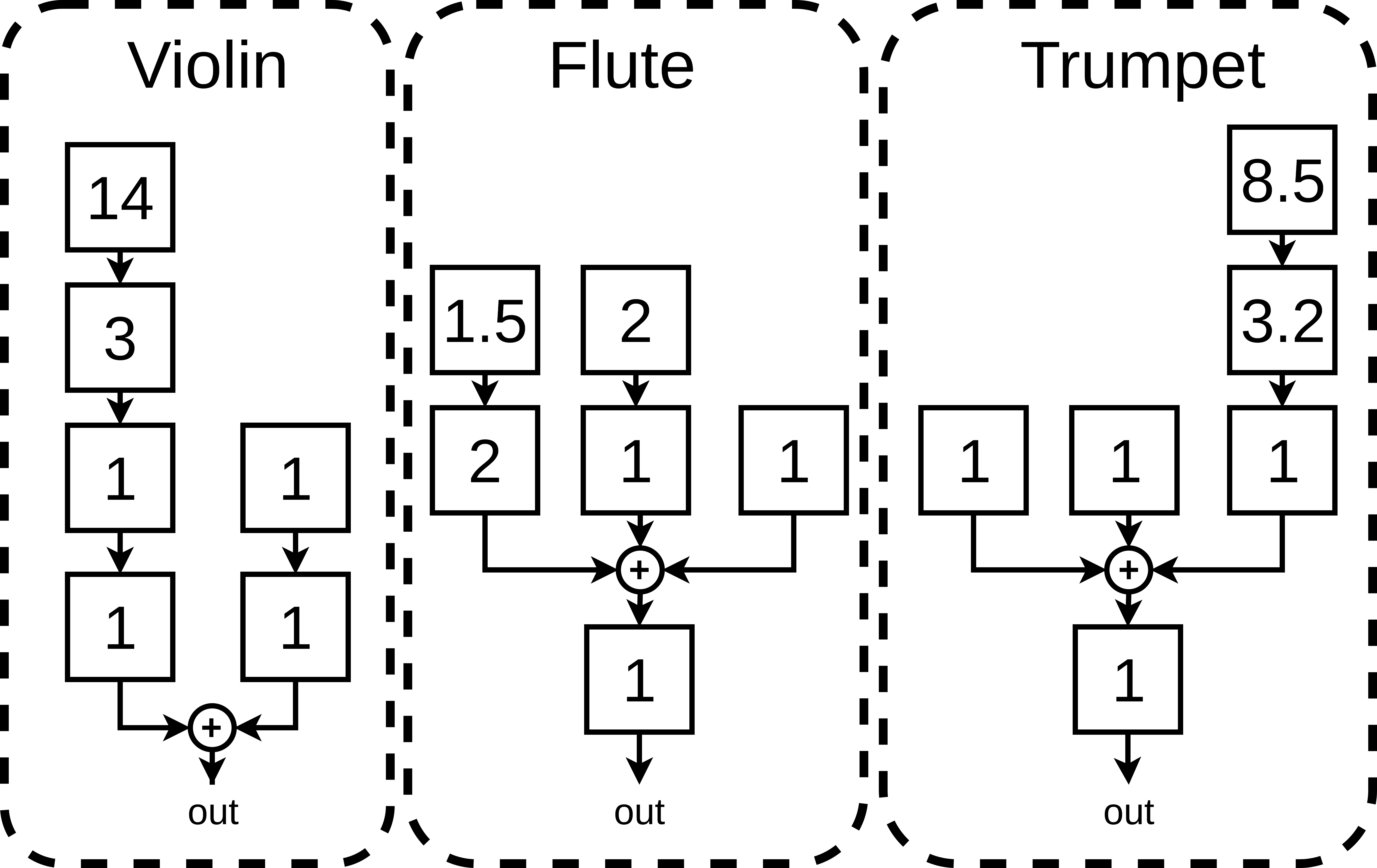
Maximum Modulation Index Test

We observe that I_max is an important hyperparameter for DDX7. A wrong selection may hinder model convergence, with results sounding unnatural, and the optimization process failing at the estimation of the room response. We leave further analysis of the impact of I_max and the Learnable Reverb on the training process for future work.

Model	Flute	Violin	Trumpet
Original
HpN Baseline
DDX7 6 osc. I_max=2
DDX7 6 osc. I_max=2π
DDX7 6 osc. I_max=4π

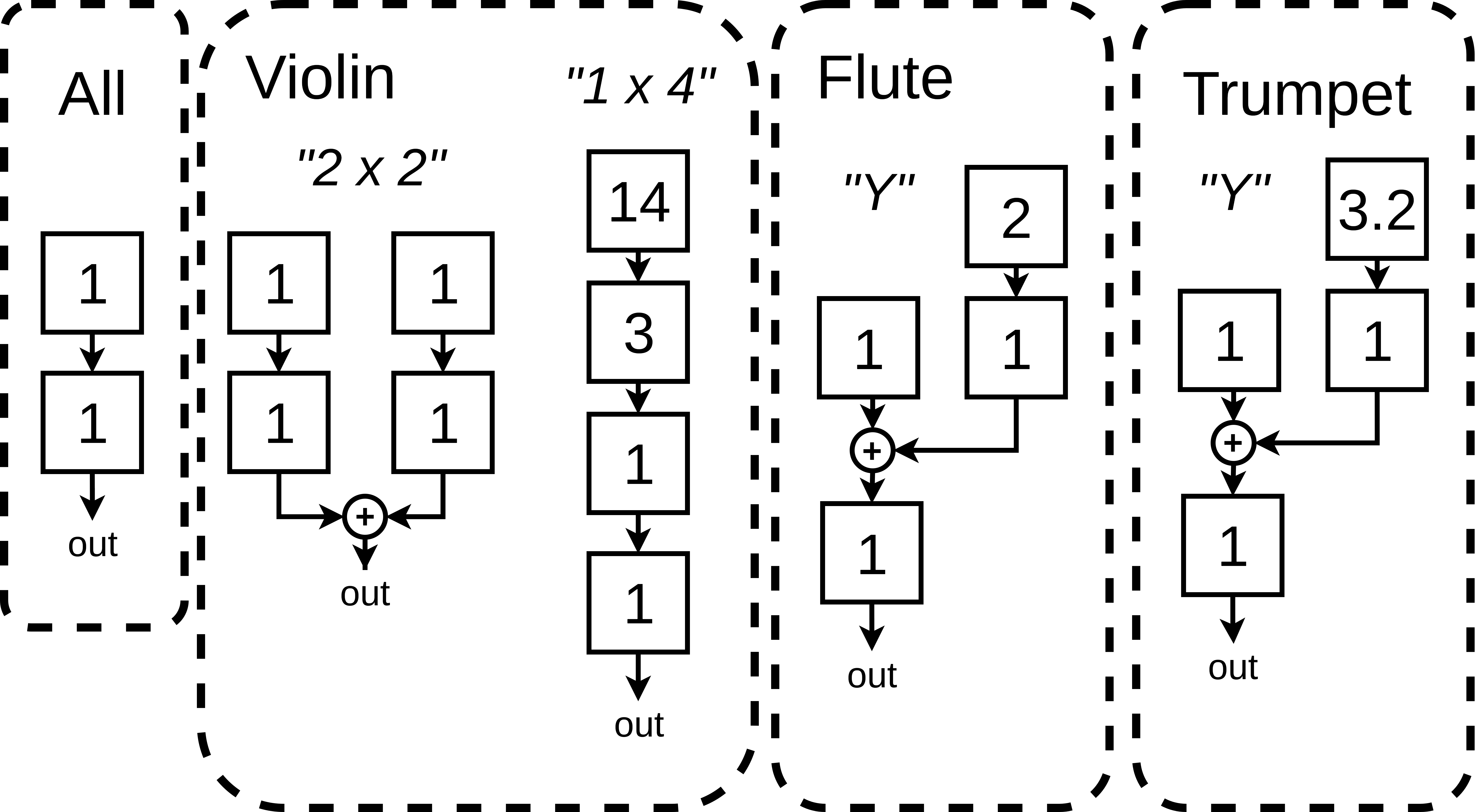
Table 3: Excerpts from the test set for different values of I_max tested.

Oscillator Ablation Test

For Violin and Flute, we observe that the models benefit from the extra degrees of freedom present with more oscillators. Surprisingly, for Trumpet, we achieve the best results with a simple 2-oscillator FM configuration, even outperforming the baseline, which suggests that good results can be obtained even with very simple configurations.

Instrument	6 oscillators	4 oscillators "Y"	4 oscillators 4x1	4 oscillators 2x2	2 oscillators
Flute I_max=2
Violin I_max=2
Trumpet I_max=2π

Table 4: Excerpts from the test set evaluated on the ablated models.

Real-time Factor test

Due to lack of space in the paper, we left out a comparison of the real-time factor between our DDX7 model (400k parameters) and the HpN Baseline (4.5 M parameters). We execute on Pytorch the inference of audio excerpts of different length (to accomodate for different latencies) for both our model and the baseline on a laptop CPU ( Intel i7-6700HQ ). We render the audio excerpts a hundred times and extract the Real-time Factor according to the following formula, extracting the mean and standard deviation of the runs.

rt_factor = time_to_compute / length_of_audio_generated

An algorithm that can operate on real-time has to have a real time factor smaller than 1. The results shown in Table 1 indicate that DDX7 can run with as little as 32 ms of latency in real time on a laptop CPU, but the HpN Baseline needs at least 128 ms. These metrics can be improved further for both models if a different framework is used (for instance, TorchScript).

	Real Time Factor
Latency (ms)	DDX7	HpN Baseline
256	0.079 (0.005)	0.231 (0.0124)
128	0.158 (0.011)	*0.466 (0.0229)*
64	0.343 (0.039)	1.04 (0.192)
32	*0.637 (0.042)*	1.88 (0.111)
16	1.31 (0.169)	3.71 (0.188)
8	2.51 (0.161)	7.39 (0.32)
4	5.01 (0.215)	15.2 (1.19)

Table 5: Mean and std (in italics) of the Real-time Factor for DDX7 and the HpN Baseline. Minimum feasible latencies are shown in bold for both models.

References

K. Kilgour, M. Zuluaga, D. Roblek, and M. Sharifi, “Fréchet Audio Distance: A Reference-Free Metric for Evaluating Music Enhancement Algorithms,” in Interspeech 2019. ISCA, Sep. 2019, pp. 2350–2354.
B. Li, X. Liu, K. Dinesh, Z. Duan, and G. Sharma, “Creating a Multitrack Classical Music Performance Dataset for Multimodal Music Analysis: Challenges, Insights, and Applications,” IEEE Transactions on Multimedia, vol. 21, no. 2, pp. 522–535, Feb. 2019.
J. Engel, L. H. Hantrakul, C. Gu, and A. Roberts, “DDSP: Differentiable Digital Signal Processing,” in 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020.